The Circle of Fifths Can Help You Make Better Music - Here's How

The Circle of Fifths is one of the most fascinating concepts in music theory.

It somehow manages to be both incredibly simple and mind-numbingly complex, depending on the context.

That said, mastering (or at least thoroughly understanding) this musical tool will make you a better musician, composer, producer, and songwriter.

In this post, you’ll learn:

What the Circle of Fifths is and how it works.
How the Circle of Fifths can unlock more sophisticated songwriting and composition.
Some examples of how to use the Circle of Fifths.

Let’s dive in!

Table of Contents

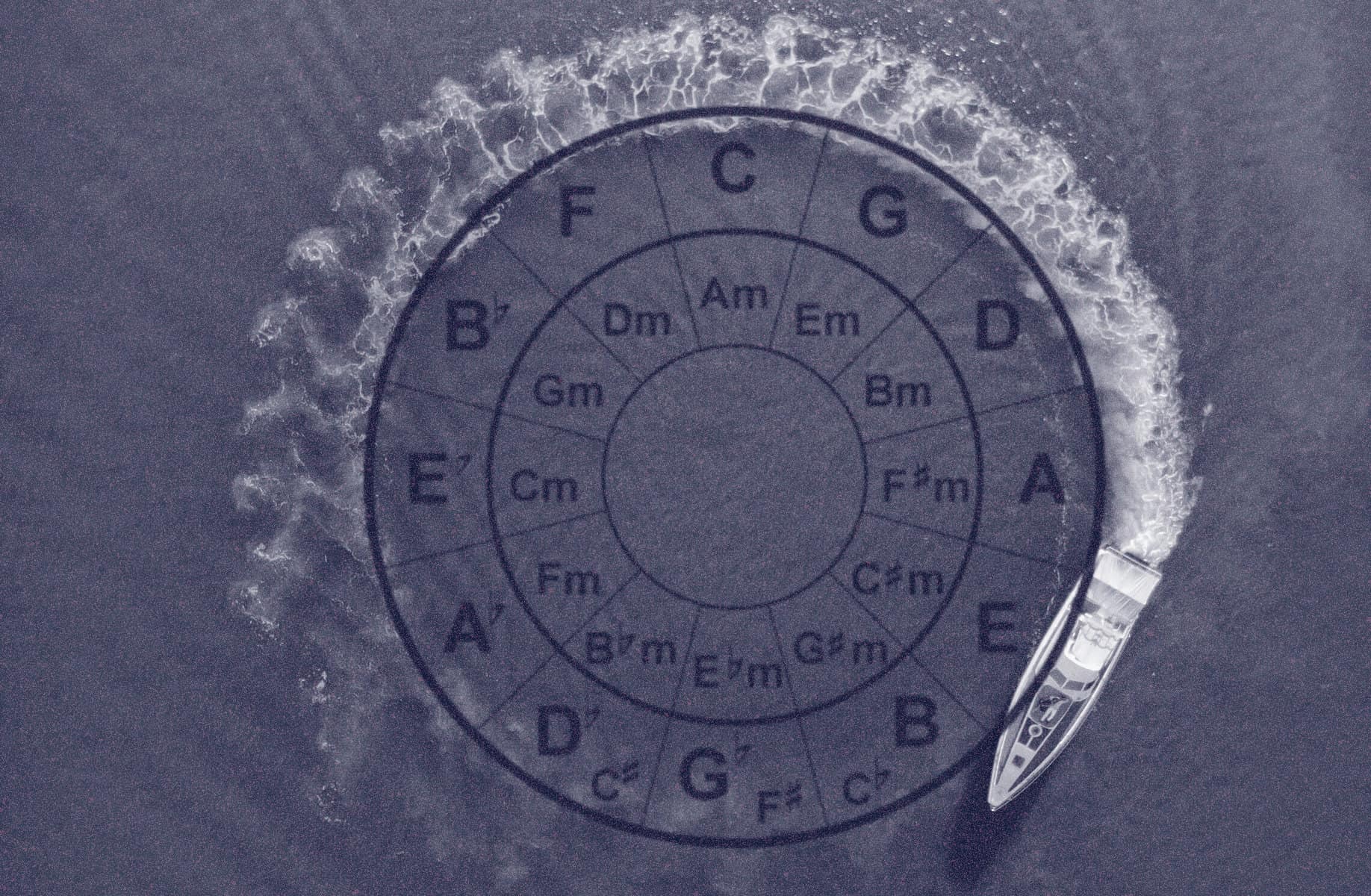
What is the Circle of Fifths?

The Circle of Fifths is a musical tool that helps explain the relationship between keys and notes. It can be used to figure out key signatures, compose new music, or transpose existing music into different keys.

Perhaps the most important thing the Circle of Fifths teaches is how different keys relate to each other.

The circle is a visual representation of all 12 major keys in Western music (technically 30 if you count minor keys and enharmonic spellings of certain keys… but let’s not get ahead of ourselves).

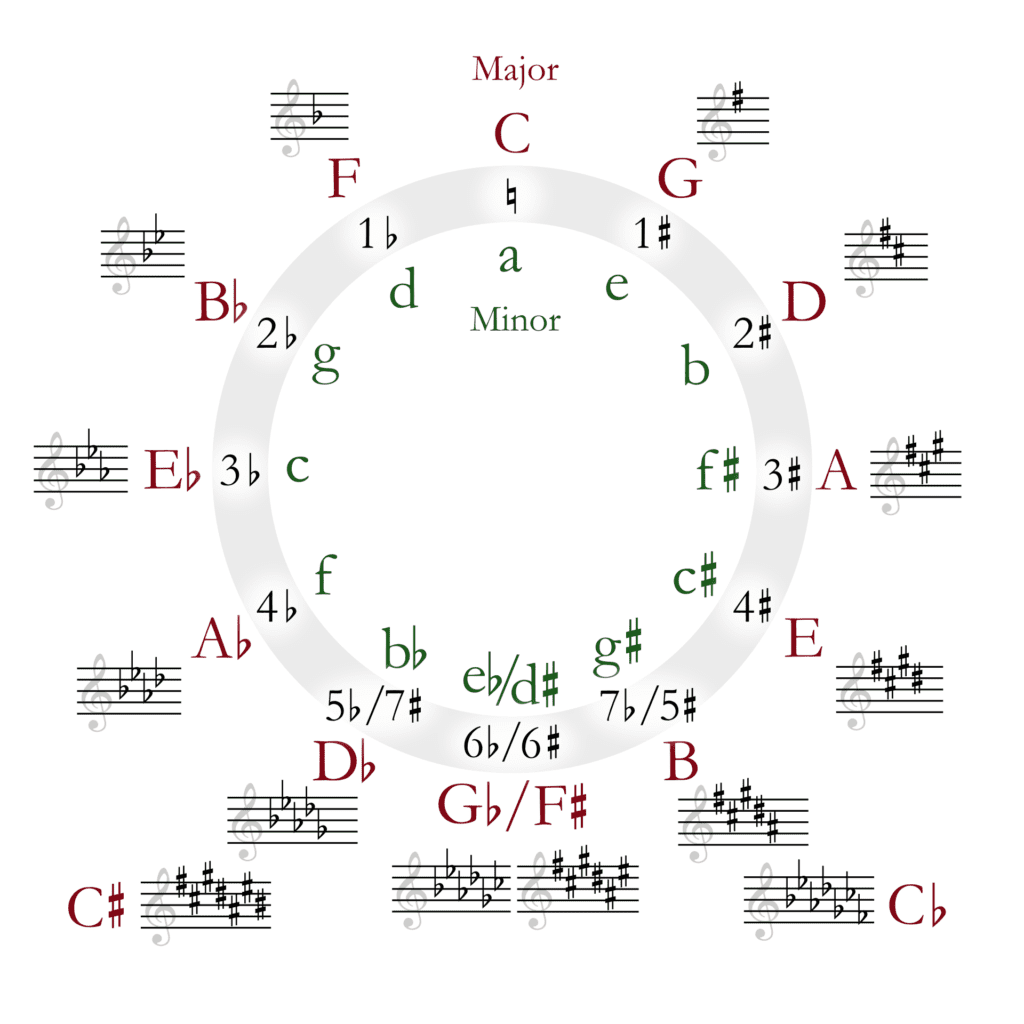
Why is it called the Circle of Fifths?

The circle of fifths gets its name from the fact that it is arranged in a circular fashion, with each key being a perfect fifth away from the last.

(Or a perfect fourth if you’re moving counter-clockwise.)

A perfect fifth is an interval (two notes) that is seven semi-tones (or half-steps) apart. Sitting down at a piano is a great way to visualize this.

Starting on a C note, we can count up 7 keys (including the black keys) and we’ll land on G.

If we did the same from G, we’ll land on D. From D, we land on A, and around the circle, we go until we get back to C.

Minor keys on the Circle of Fifths

Just as there are major keys on the circle, there are also minor keys. The minor keys are arranged in the same order as the major keys (notated in the inner circle in the above graphic).

So, if you start in C minor, the next key would be G minor, followed by D minor, and so on.

How does the Circle of Fifths work?

Each key is represented by a point on the circle, and the distance between two clockwise keys (like C and G, for example) is a perfect fifth.

Note that if you were to move counter-clockwise (like from C to F), you’d actually be moving in perfect fourths. But, as soon as you reverse direction and start moving clockwise again, you’re back to moving around in fifths.

It feels a bit like an optical (or, in this case, audible) illusion. 🤔

Generally speaking, if one starts at C major, moving along the circle clockwise takes you into the sharp keys, and moving counter-clockwise takes you into the flat keys.

For example, the key of C major has no sharps or flats. The key of G major is one clockwise move away from C major, therefore it has one sharp.

The key of D is two clockwise moves away from C, therefore it has two sharps.

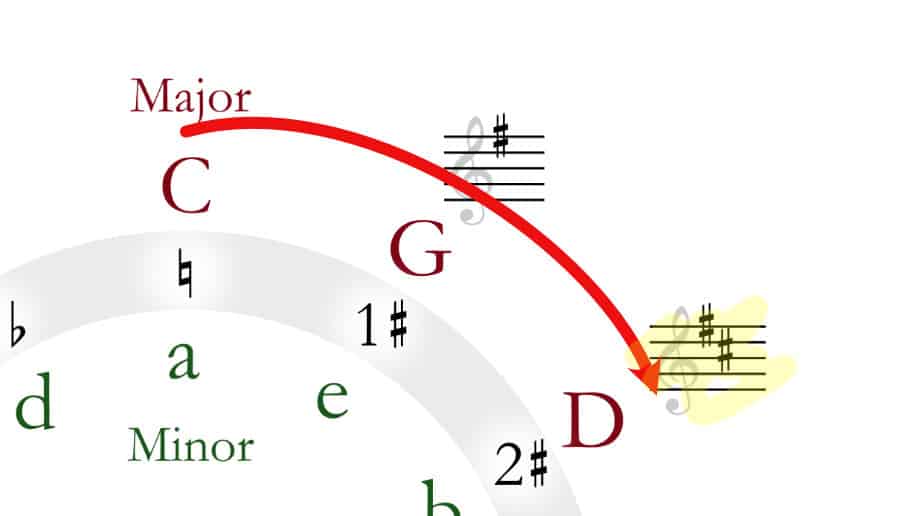
Keys that move clockwise increase in the number of sharps, while keys that move counter-clockwise increase in the number of flats.

For example, F is one move counter-clockwise from C. That means it has one flat. Ab is four moves counter-clockwise from C, which means it has four flats.

If you’re wondering, “how in the heck will this help me make better music?” Stick with me. Things are about to get very practical.

How to use the Circle of Fifths

The Circle of Fifths can be used to figure out key signatures, compose new music, or transpose existing music into different keys.

It’s also extremely handy for developing modulations and interesting chord progressions.

Using the Circle of Fifths to figure out key signatures

Let’s say you’re honing your composition, music theory, and production skills by studying lead sheets and scores.

You download a piece of music and you’re greeted by this.

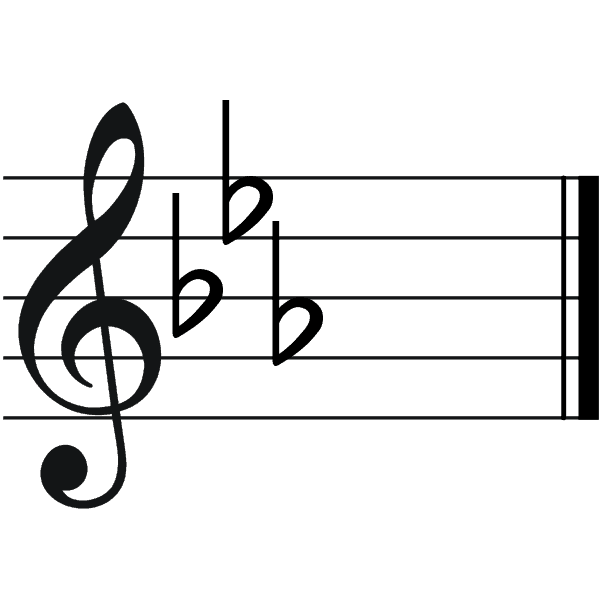
You stare at it like a deer in headlights. You pace your house in a deep malaise. You reminisce on the beautiful simplicity of your childhood and wonder if it’s all worth it.

No, it’s really not that serious, because you can use the Circle of Fifths to quickly figure out this key signature without any hunting and pecking on the piano.

Simply observe how many sharps or flats the key signature has, and count that number of steps either clockwise or counter-clockwise from C.

For example, this piece has three flats. We know that keys increase in flats as they move counter-clockwise from C. So, we move three spots counter-clockwise from C.

Boom, we’re in E♭.

Real quick: I have a course all about composing game music for beginners. One of my video lessons is all about the Circle of Fifths. Check it out for free via the button below!

Check out the lesson here!

Using the Circle of Fifths to compose new music

Let’s say after analyzing our piece in E♭ major, we want to try our hand at composing our own piece in the same key.

The good news is that the Circle of Fifths can also tell us which chords typically go well together.

This lovely interactive Circle of Fifths tool saves us a lot of hard work. As you can see, the chord counter-clockwise to the target key is the IV of that key.

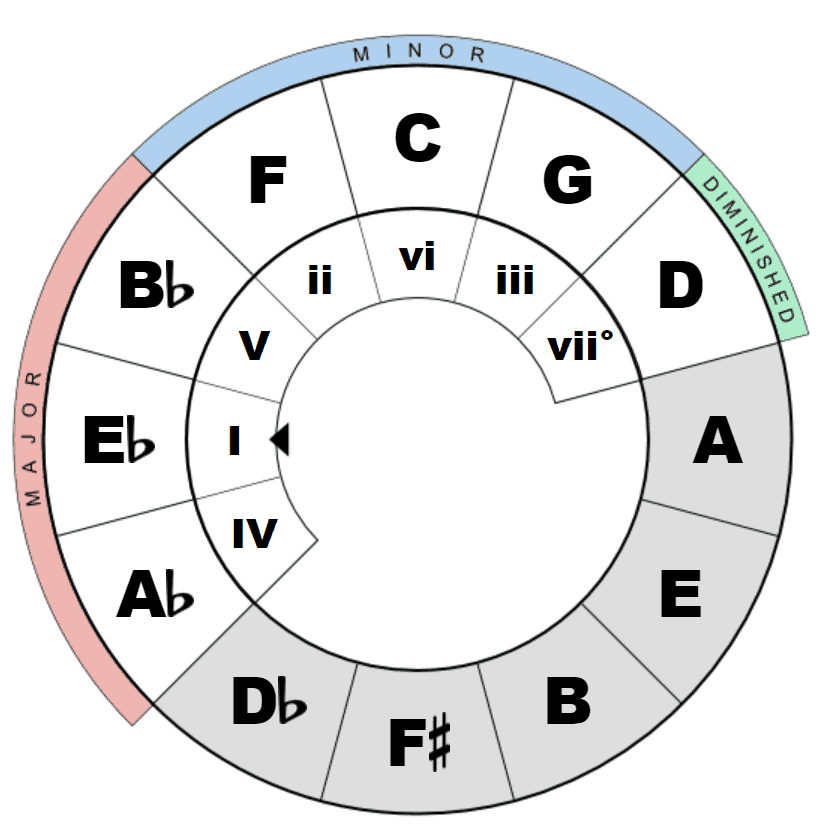
Moving clockwise, the scale degrees are:

Bb (V)
F (ii)
C (vi)
G (iii)
D (vii°)

Funny enough, if we were to start from the vii° (in the case of E♭, that’s a D°), and move counter-clockwise back through the Circle of Fifths to our target key (the E♭), we’d be playing a very common jazz chord progression, the “7, 3, 6, 2, 5, 1.”

And, to keep things even and symmetrical, we’ll add the fourth (A♭) there at the beginning of the chord progression.

Here’s what that sounds like (with some nice seventh extensions):

Are you starting to see how practical the Circle of Fifths can be for composition?

Using the Circle of Fifths to transpose music

You can also use the circle of fifths to transpose music into different keys.

This comes in exceptionally handy when you’re playing with a band or singers who need a tune to be more in their range.

For example, if you have a song in C major but want to sing it in D major, you can use the circle of fifths to figure out what chords sound best together by simply shifting the whole formula over.

(Once again, the interactive Circle of Fifths tool does a great job of visualizing this.)

Using the Circle of Fifths to modulate intelligently

Modulation is simply the act of changing from one key to another.

This can be done in many ways, but one of the most common (and effective) ways to do it is by using the Circle of Fifths.

For example, if we’re in the key of C major and want to modulate to a new key, the Circle of Fifths can not only tell us which chords will sound good in our new key but also how jarring the modulation will feel to the listener.

Here’s what I mean.

In the case of C major, the two major keys that are the most related are F and G. And yes, these are the keys that just happen to be the left and the right of C. Both F and G share many of the same chords and almost all of the same notes as C.

Therefore, a modulation from C major to F major or G major would be “smooth,” and not very drastic-sounding to the listener. In this context, we’d call these adjacent keys.

Listen to this audio sample of a chord progression in C modulating to the key of G:

Here’s another way of saying it: as a general rule, the further away from your home key you modulate, the more jarring it will sound.

To illustrate this point, let’s look at the furthest possible key from C on the Circle of Fifths. As we can see, that’s an F# (or G♭).

This is a tritone interval, which is commonly regarded as one of the most dissonant intervals in music. The way you find a tritone is just by drawing a straight line across the Circle of Fifths, like so:

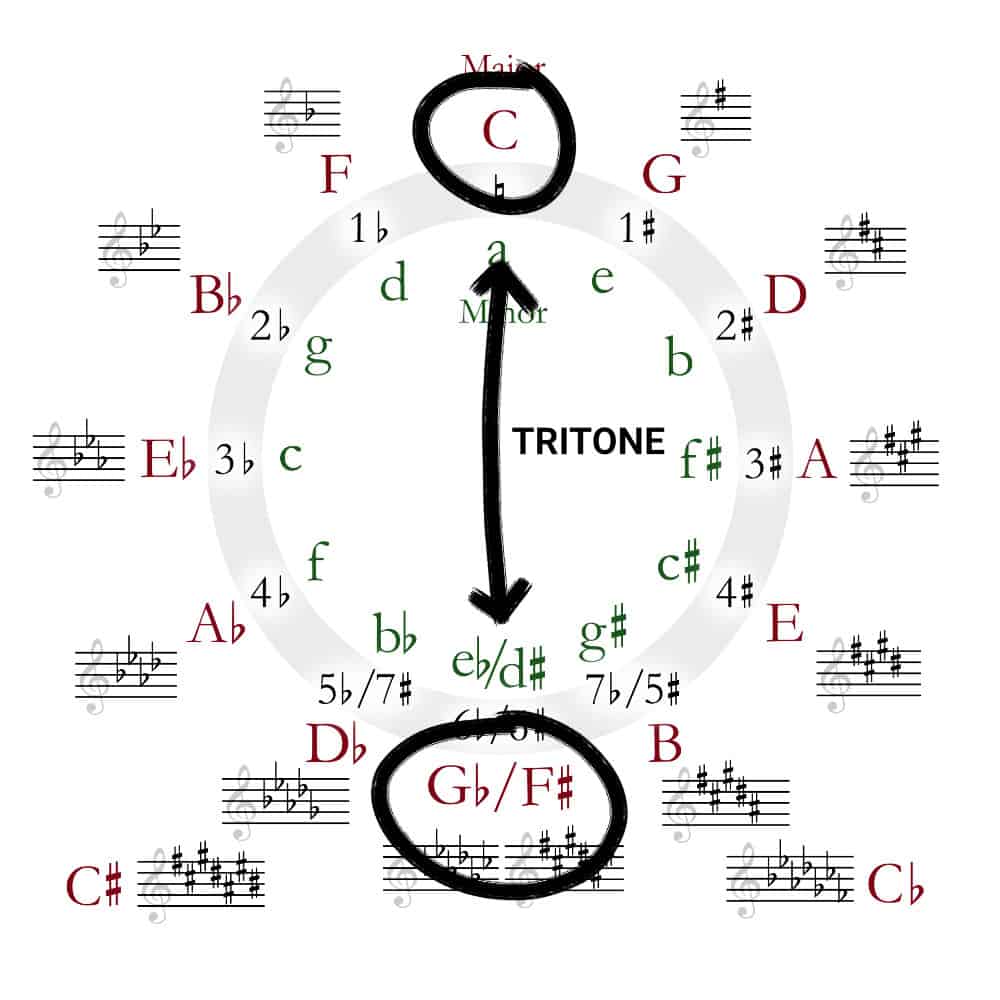
Now, listen to this audio sample of a chord progression in C modulating to F#:

Pretty stark contrast, eh? But that’s not always a bad thing! Tension is an essential part of music, especially in the world of film, games, and media composition.

Using this tritone modulation trick may be just what your piece needs to amp the tension up to 11!

(And by the way, this modulation principle works just as well with minor scales as it does with major scales!)

Using the Circle of Fifths to identify relative minor chords

Finally, the Circle of Fifths can also help us find the relative minor chords of each major chord (or relative major chords of each minor chord).

(Yep, the Circle of Fifths is helpful for both major and minor keys.)

A relative minor chord is simply a minor chord that shares the same key signature as its major counterpart.

The same principle applies to relative minor keys.

For example, the relative minor key of C major is A minor, because they both have no sharps or flats in their key signatures.

The relative minor of D♭ major is B♭ minor because they both have five flats in their key signatures.

To find the relative minor chord using the Circle of Fifths, all we need to do is count three spaces clockwise from our target major key.

A is three spaces clockwise from C, and B♭m is three spaces counter-clockwise from Db. Therefore, Am is the relative minor of the key of C major, and B♭m is the relative minor of the key of D♭.

It’s worth mentioning that although these keys share the same notes, they have a different tonal center, which makes them technically different keys.

Should you memorize the Circle of Fifths?

Should you memorize the entire Circle of Fifths? Probably not, but it may be helpful.

Yes, you should definitely familiarize yourself with the Circle of Fifths; it’s an extremely useful tool that will make writing songs easier and more fun.

But despite what music theory textbooks may say, you don’t need to have it memorized in order for it to be useful to you.

In fact, I would argue that trying to memorize the Circle of Fifths is actually counter-productive because it’s much more important to understand how it works than simply being able to recite it from memory.

That being said, there’s nothing wrong with memorizing it if it helps you understand and internalize the concept.

There are actually some pretty cool things you can do in your mind if you’ve memorized the Circle of Fifths.

For example, if you count four spaces counter-clockwise from any spot on the circle, you’ve now landed on the major third interval of that key. And that’s just scratching the surface.

Just don’t beat yourself up if you can’t quite get it down pat.

Advanced Circle of Fifths tricks

Figuring out borrowed chords using the circle of fifths

One of the more advanced applications of the Circle of Fifths is using it to figure out borrowed chords.

Borrowed chords are simply chords that are “borrowed” from other keys in order to create a little bit of tension or interest in otherwise bland chord progressions.

For example, let’s say we’re in the key of C major and want to add a little bit of flavor to our tune.

As a refresher, the diatonic chords in C major are C, Dm, Em, F, G, Am, and Bdim.

We can “borrow” a chord from the parallel minor key. A parallel minor key is simply the minor key that shares the same tonic as our major key. In this case, that’s C minor.

The chords in C minor are Cm, Ddim, E♭, Fm, Gm, A♭, and B♭.

A very common progression to evoke a sense of ascension or victory is ♭VI (A♭) – ♭VII (B♭) – C (I). You’ve certainly heard it before, such as in the intro of With a Little Help From My Friends by the Beatles (“Biiiiilllllyyyy Sheears!”):

As well as in the iconic Victory Theme from Super Mario Bros:

The great thing about using the Circle of Fifths to find borrowed chords is that once you memorize the formula, you can apply it to any key. Music theory is mathematical and symmetrical, after all!

For example, to find the two chords used in this progression (the ♭VI and ♭VII), you simply move two spaces counter-clockwise (that’s your ♭VII) and then four spaces counter-clockwise (that’s your ♭VI).

In the case of C major, that’s B♭ and A♭.

Now, when you’re composing or playing a song in D major, you won’t be limited by having to do a bunch of theory math in your head. You can pull up the Circle of Fifths and apply the formula.

How other musicians think through the Circle of Fifths

A lot of really smart musicians have spent stupid amounts of time studying the Circle of Fifths.

One of the most popular new approaches to the Circle of Fifths came from the prodigious Jacob Collier. He calls it “negative harmony,” and it’s a fascinating concept introduced via this YouTube video a few years back.

As you may imagine, the theory geeks still go nuts over this stuff:

Victor Wooten also makes a compelling case that the Circle of Fifths actually contains 30 keys, not 12.

Also, he shows that the number of flats and sharps across parallel keys are all perfect mirrors of each other.

This kind of blew my mind when I first watched it, so check it out here:

Conclusion

The circle of fifths is a valuable tool for any musician, regardless of experience level.

Understanding the Circle of Fifths can help musicians compose more fluidly and improvise more creatively. It can also aid in the development of a stronger sense of tonality and an increased understanding of music theory.

There are many benefits to using the circle of fifths. By understanding how chords are related to each other, you can compose new music or transpose existing music into different keys. You can also use the circle of fifths to help you understand key signatures and guitar chords.

If you want to go deeper into the practical steps of composing game music, check out my course here.

Or, if you want grow in your musical composition skills, check out these related posts:

FAQs about the Circle of Fifths

Here are some frequently asked questions about the Circle of Fifths (and related music theory topics):

What is a diatonic scale?

A diatonic scale is a musical scale that consists of seven distinct pitches or notes. These seven notes are arranged in a specific pattern of whole and half steps, with two of the steps being half steps and the rest being whole steps. This pattern of steps produces a unique sequence of intervals between the notes, which is the defining characteristic of the diatonic scale.

In Western music, the most common diatonic scale is the major scale, which follows the pattern of whole-whole-half-whole-whole-whole-half. The seven notes in a diatonic scale are named using the letters A through G, and each note is given a unique name that reflects its position within the scale.

Diatonic scales are the building blocks of Western music, and they are used to create melodies, harmonies, and chord progressions. They provide a sense of tonality or key, and they are the foundation upon which much of Western music is built.

What is a major triad?

A major triad is a chord consisting of three notes: the root, the third (major third), and the fifth (perfect fifth), played simultaneously.

What is a circle progression?

A circle progression (also known as a circle of fifths progression) is a chord progression in which each chord contains a note that is a fifth (or fourth) higher than the previous chord. This creates a circular pattern when the progression is written out.

What does equal temperament mean?

Equal temperament is a tuning system in which the octave is divided into 12 equal parts, each separated by a ratio of the 12th root of 2. This means that the frequency ratio between any two adjacent notes (also known as semitones) is the same, which creates a system of equal intervals between pitches.

In equal temperament, all 12 notes in Western music are equally spaced, which allows for modulation between different keys and a greater range of tonal possibilities. This system is commonly used in modern Western music, as it allows for easy transposition of music between different keys and ensures that all notes sound in tune regardless of the key.

However, the equal temperament system does not produce the pure intervals that are created in other tuning systems, such as just intonation or Pythagorean tuning. This can result in some intervals and chords sounding slightly out of tune or less harmonically related, but the benefits of being able to play in any key without retuning have made equal temperament the most commonly used tuning system in Western music.

What’s the difference between a key and scale?

The key refers to the tonal center of a piece of music, while the scale refers to the collection of pitches used in that key. Western scales are typically made up of seven notes, each separated by a pattern of whole and half steps.

What is pitch class?

A pitch class is a group of all pitches that share the same letter name (e.g. all C’s, regardless of octave).

What is just intonation?

Just intonation is a tuning system in which the frequency ratios of pitches are based on small whole numbers, such as 1:2 (octave), 2:3 (fifth), and 3:4 (fourth). This produces pure intervals that are harmonically related and have a clear and distinct sound.

In just intonation, the intervals between notes are not equal in size, as they are in the more common equal temperament system. This can result in some keys sounding more in tune than others, as certain intervals may not align perfectly with each other in all keys.

Just intonation is commonly used in some styles of non-Western music, as well as in the performance of early Western music. However, it can be difficult to achieve in modern Western music, as it requires precise tuning and can sound out of tune in some keys.

What is Pythagorean tuning?

Pythagorean tuning is a tuning system in which the frequencies of pitches are based on the ratios of the first few prime numbers, particularly the ratios of 2:1 (octave) and 3:2 (fifth).

In Pythagorean tuning, the octave is divided into a series of perfect fifths. Each new pitch is derived from the previous one by multiplying its frequency by 3/2. This process is repeated until the desired pitch is reached, which creates a sequence of pitches that are harmonically related and have a pure and clear sound.

What are double sharps?

A double sharp is a musical symbol that looks like an “x” and indicates that a note should be raised by two semitones (or a whole step). In other words, it is a note that is sharpened twice.

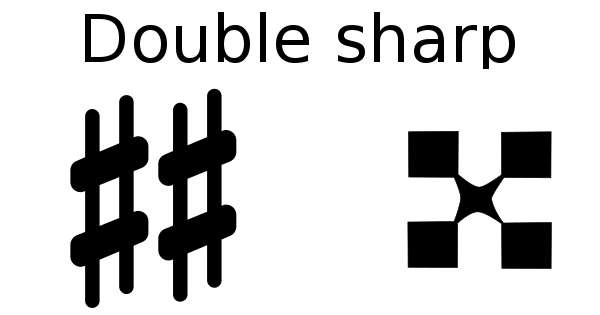
Double sharps are used to notate notes that are not diatonic to a key, or to indicate a specific chromatic alteration of a note in a chord. For example, in the key of A major, the note B is normally a diatonic note (i.e., it belongs to the key), but in a chord progression where a B sharp is needed, a double sharp can be used to indicate that the note should be raised by two semitones to become a B sharp.

What’s the difference between Gb and F# (for example), and why would you use one over the other?

Gb (G flat) and F# (F sharp) are enharmonic equivalents, which means they sound the same but are notated differently. The difference between the two is purely a matter of notation.

The choice of which one to use depends on the context of the music. In some cases, one may be more appropriate than the other based on the key signature or the notes surrounding it in the music.

For example, in a piece of music written in the key of F# major, the note F# would be used instead of Gb, as it fits the key signature and is the natural note for that key. Conversely, in a piece of music written in the key of Gb major, the note Gb would be used instead of F#, as it fits the key signature and is the natural note for that key.

In some cases, the choice between Gb and F# may be based on the harmonic function of the note in a chord progression. For example, in a chord progression where the dominant chord is F#7, the note F# would be used in the chord rather than Gb, as it is the natural note for that chord and provides the desired harmonic function.

Another reason why a composer may choose to use one enharmonic spelling over the other is that it may be easier to read for musicians. This is particularly true in cases where one notation would require multiple double sharps or double flats, which can be confusing and difficult to read for inexperienced sight readers.

For example, in a piece of music written in the key of Gb major, using the note F instead of E# can make the music easier to read.

This is because in Gb major, the notes Bb, Eb, and Ab are already in the key signature, which means that if the note E# is used, it would require a double sharp symbol to maintain the diatonic nature of the key signature.

By using the note F instead, the music becomes easier to read as it eliminates the need for a double sharp symbol.

Overall, the choice between enharmonic spellings may be influenced by a variety of factors, including the key signature, harmonic function, and ease of reading for musicians.

By choosing the most appropriate enharmonic spelling, a composer can ensure that their music is not only musically accurate, but also easily readable and playable for musicians.